MVLib - Short Writeup - Version 4.0
Manipulating 1D and 2D arrays using Cellular Automata approach
Last update: August, 20 2013
Source code available for local users only
The following routines allow to manipulate 1-dimensional and 2-dimensional arrays characterized by continuous values.
d2cellcycle(matr,rule,work,ix,jx,alpha) This routine carry out a cycle of evolution on the input real matrix matr(ix,jx) passed as first argument, the input integer array rule(ix,jx)contains the rules of evolution, while real array work(ix,jx) is a work array, the last argument is real coefficient specifyng the intensity of evolution the each cycle. At each cycle each element of input array is modifield according to:
in this formula the alpha coefficient corresponds to the last argument passed to the subroutine and sum is carried out over a specific domain, such domain being specified by the integer array rule(ix,jx) more specifically:
  • rule(i,j) = 4 means that element (i,j) will evolve taking into account the status of the elements in the Von Neuman domain, namely in the 4 surrounding cells (North, East, South and West);
  • rule(i,j) = 8 means that element (i,j) will evolve taking into account the status of the elements in the Moore domain, namely in the 8 surrounding cells;
  • rule(i,j) = 0 means that element (i,j) has not to be modified, but it has to be used to modify the sorrounding cells;
  • rule(i,j) < 0 means that element (i,j) has not to be modified, and also it has not to be used to modify the sorrounding cells;
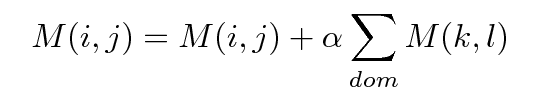
d1cellcycle(vec,rule,dummy,n) The routine d1cellcycle is similar to previous one, but it works on a one-dimensional array vec(n). In this case the rules are specified in the integer vector passed as second argument with the following meaning:
  • rule(i) = 2 means that element (i) will set with the average of the two adjacent elements;
  • rule(i) = 0 means that element (i) has not to be modified.
Note that you have iterate the call to this routine few time the number of maximum consecutive component you have to fill; as an example to obtain a sequence a hourly data from the daily average you have to call this routine at least 100 times.
The third argument is a dummy argument for backward compatibility only and is NOT used by the routine.
cavectorfill(v,w,z,ndat) This routine allows to fill the input real vector v(n) replacing the values -9999.0, usually marking a no-data value, with a value obtained as the average of the surrounding components of the vector (if you a sequence of more than 1 no-data values). The real vectors w(n) and z(n) are working arrays. It is used, as an example, to fill the observed time series before to plot them, see also the example 5.
The following routines allow to manipulate 2-dimensional arrays characterized by discrete values.
cellularrule (conf,rule) cellularrule allows to define the evolution rules for a discrete 2-dimensional cellular automata system, to this aim you have to specify the rules of evolution for each possible configuration. The first integer argument specifies the configuration and the second integer argument specifies the rule associated to this configuration. The cofiguration are coded taking into account the status of each bit, and the bits are numbered clockwise from north-west (1) to west (8), as an example the configuration where only the third bit is on is "called" 4, because it corresponds to the bit configuration 00000100, if you want to specify the evolution rule for this configuration you have to call cellularrule specifying 4 as first argument. The second argument is coded value specifying the rule of evolution, more specifically:
  • R=0 means that the status of the cellular automaton have not to be changed with this configuration, this is the default for all the 256 possible configurations;
  • R=1 means that the status of the cellular automaton must be "ON";
  • R=-1 means that the status of the cellular automaton must be "OFF";
  • R=2 means that the status of the cellular automaton must changed and it will be "ON" if it was "OFF" and viceversa;
  • R=11-18 means that the status of the cellular automaton must changed to the R-10th bit in the neightborhood;
  • R=20 means that the status of the cellular automaton must be the average of the status of the cellular automata in the neightborhood;
For what concerns the application the rules 0, 1, -1 and 2 allow to manipulate digital systems, while rules 11-18 and 20 allow to manipulate analogic values.
NB:
The special value -1 for the first argument automatically allows to assign the rules of "Life game", in this case the second argument is ignored. See also the examples 38 and 40.
The special value -2 for the first argument automatically allows to assign the rules for digital signal filtering, in this case the second argument is ignored. See also the example 39.
cellularinit(mat,m,n,type,xc,yc) This routine allows to fill the array mat(m,n) with few standard macrostructures allowing to produce funny dynamical effects with Langton "Game of Life" rules; the kind of structure is specified by the integer parameter type passed as 4th argument (it must be in the range 1-3), the structure is created around the element of the matrix specified by the last two integer arguments. See also the examples 38 and 40.
cellularcycle(mat,m,n) After defining the rules of evolution using cellularrule, this routine is invoked one or several times to preform a "life cycle" modify the integer input array mat(m,n).
cellularplot(mat,m,n) This routine allows the plot the cellular automata system contained in the integer input array mat(m,n) passed as argument. See also the examples 38, 39 and 40.
cellularplotrule(flag,str) Depending on the integer flag passed as argument, this routine allows to plot the naming of the rules (flag=0) or the rules defined at the current step (flag=1). The second argument is a string that will be used as prefix for the filename that will be created. See also the example 34.
MVLib documentation version 4.0 created by Marco Verdecchia This document has been updated on February 27, 2013 h: 11.11