In questo lavoro viene presentata e discussa una metodologia innovativa di validazione Lagrangiana di correnti marine, misurate con tecniche satellitari, nell’ambito del progetto GlobCurrent dell’ESA (Agenzia Spaziale Europea). La tecnica si basa sullo studio delle proprietà di dispersione di traiettorie numeriche calcolate utilizzando come input i campi di velocità da validare in un modello Lagrangiano.
I moti turbolenti nel modello, non risolti dalla dinamica a grande scala, sono simulati con moderne tecniche cinematiche che ristabiliscono la statistica della dispersione a media e piccola scala. La metodologia di validazione è innovativa in quanto la qualità del dato satellitare di velocità viene valutata non con un normale confronto, punto per punto, con dati in situ (approccio Euleriano) ma analizzando e confrontando le caratteristiche delle traiettorie Lagrangiane numeriche con le traiettorie vere delle boe di superficie (approccio Lagrangiano). Questo perché, in generale, è noto che a campi di velocità simili (con differenze anche minime, dell’ordine dell’errore sperimentale) possono corrispondere traiettorie di particelle di fluido molto diverse tra loro, a causa della non linearità della dinamica e del caos deterministico, ovvero la elevata sensibilità delle soluzioni agli errori iniziali.
Normalmente l’errore tra simulazione e osservazione cresce con la scala di separazione (e quindi nel tempo). Recenti sviluppi della teoria dei sistemi dinamici consentono di applicare tecniche di misura della crescita dell’errore in funzione della scala (FSLE), e, parallelamente, di compensare il contributo mancante dei moti turbolenti non risolti con parametrizzazioni dinamiche definite in termini di sistemi caotici multi-scala. Con questa procedura si ottengono tre risultati fondamentali: 1) la misura delle proprietà di dispersione di traiettorie a parità di dinamica (predicibilità di primo tipo); 2) la misura dell’errore tra simulazioni e osservazioni su tutte le scale del moto accessibili (predicibilità di secondo tipo); 3) la calibrazione su dati in situ (boe Lagrangiane di superficie) della parametrizzazione dinamica turbolenta per ottimizzare le simulazioni di traiettorie dai prodotti satellitari sottoposti a validazione.
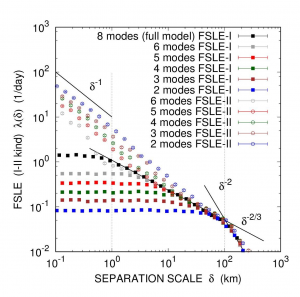
Fig. 1: Test di validazione Lagrangiana sul modello cinematico di prova. Il modello base è caratterizzato da 8 modi spaziali (armoniche di Fourier) distribuiti su due decadi. I modelli approssimati hanno risoluzione decrescente da 6 a 2 modi. L’FSLE di I tipo calcola il tasso di dispersione relativa delle traiettorie dei singoli modelli; l’FSLE di II tipo calcola la crescita dell’errore tra modello approssimato e modello base. Gli scaling si riferiscono rispettivamente a: diffusione balistica (-1); diffusione turbolenta (-2/3); diffusione standard (-2). Il plateau dell’FSLE indica separazione esponenziale a tasso costante, indipendente dalla scala. I simboli neri rappresentano la dispersione relativa di riferimento del modello base. La scala di overlap tra FSLE di I e II tipo è la scala soglia oltre la quale gli errori dovuti al modello sono riassorbiti dagli errori dovuti alla non linearità intrinseca della dinamica.
Sono stati considerati tre casi studio: I) un modello cinematico di prova (Fig. 1) su cui testare la tecnica di validazione; II) il Mar Mediterraneo (Fig. 2); III) l’Oceano Atlantico settentrionale (Fig. 3). La particolare scelta dei casi applicativi (II e III) è motivata dalla possibilità di testare le caratteristiche dei campi di velocità misurati da satellite (altimetro) su domini spazialmente molto diversi, con campi a risoluzione diversa e a composizione diversa (con e senza termine di trasporto Ekman), e con differenti proprietà di dispersione relativa di mesoscala (diffusione turbolenta per il Mediterraneo, diffusione balistica per il nord Atlantico).
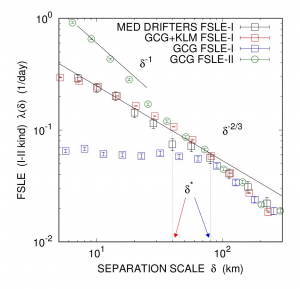
Fig. 2: Mar Mediterraneo. Crescita degli errori di I e II tipo: dispersione di boe Lagrangiane (quadrati neri); dispersione di traiettorie simulate GlobCurrent (quadrati blu); dispersione traiettorie simulate GlobCurrent con parametrizzazione dinamica della turbolenza (quadrati rossi); tasso di crescita dell’errore tra traiettorie simulate e traiettorie vere (cerchi verdi). La parametrizzazione della turbolenza permette un migliore accordo tra dispersione relativa simulata (GlobCurrent) e dispersione vera (boe). La scala δ* rappresenta la soglia oltre la quale gli errori dovuti alla risoluzione finita del dato satellitare sono riassorbiti dalla non linearità intrinseca della dinamica. I campi di velocità GlobCurrent utilizzati in questo caso studio comprendono la sola componente geostrofica (altimetro).
Complessivamente i risultati ottenuti alla fine del test di validazione indicano che i prodotti satellitari GlobCurrent analizzati in questo lavoro, dal punto di vista Lagrangiano, sono qualitativamente paragonabili o superiori a campi di velocità prodotti da modelli di circolazione generale, a parità di risoluzione. Il vantaggio nell’utilizzo di prodotti satellitari risiede nell’ampia copertura spaziale e temporale dei dati e nella loro accessibilità attraverso le piattaforme web delle agenzie che li gestiscono. Risulta quindi fondamentale avere uno strumento matematico-operativo, complementare alle normali procedure di validazione di tipo Euleriano, in grado di valutare la qualità del prodotto in senso Lagrangiano, misurando la crescita degli errori tra traiettorie vere e simulate in funzione della scala di separazione.
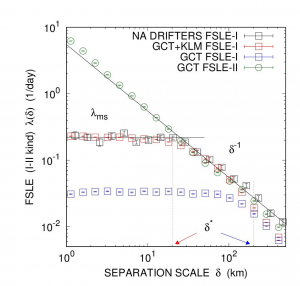
Fig. 3: Nord Atlantico. Crescita degli errori di I e II tipo (stesso significato dei simboli in Fig. 2). La scala δ* rappresenta la soglia oltre la quale gli errori dovuti alla risoluzione finita del dato satellitare sono riassorbiti dalla non linearità intrinseca della dinamica (notare la variazione di circa un ordine di grandezza con o senza parametrizzazione dinamica nelle simulazioni). I campi di velocità GlobCurrent utilizzati in questo caso studio comprendono la componente geostrofica (altimetro) più il termine di Ekman.
Autore dell’articolo: Guglielmo Lacorata
Riferimenti
G. Lacorata, R. Corrado, F. Falcini and R. Santoleri, FSLE analysis and validation of Lagrangian simulations based on satellite-derived GlobCurrent velocity data, Remote Sensing of Environment 221 (2019) 136-143, https://doi.org/10.1016/j.rse.2018.11.013

